Design & Presentation

CUNY J-School Fall 2015 | Thurs 6-8:50 | Room 434 | Lena Groeger

This course will cover the fundamentals of good presentation, layout, and design for print and the web. We'll cover basic typography, color theory, page layout, information design as well as navigation and usability. We'll explore a variety of online tools, get comfortable with Adobe Photoshop and Illustrator and introduce the languages of web design: HTML and CSS. By the end of this course you'll be able to recognize poor designs and identify how to fix them, as well as create your own designs with better organization, unity, and clarity.

CLASS ONE: OCT 8th

ANNOUNCEMENT: CLASS WILL BEGIN AT 5PM

Basic Design Principles

The things you need to keep in mind for every single project, from poster to news graphic.

← Lecture

In Class

We'll cover the four basic design principles to live by (at the end of this class you'll be very very very familiar with them.) They come straight from one of my all-time favorite design books, The Non- Designers Design Book by Robin Williams (not the actor). We'll look at examples from print and online, inside and out of the newsroom, big and small, festive and serious. We'll also do some in class design exercises and critiques to get you thinking about why — and how — design can be used to better organize, unify, and present your ideas.

The Non-Designer's Design Book

1. Proximity p 15-32

2. Alignment p 33-50

3. Repetition p 51-64

4. Contrast p 65-60

After Class

Take a resume (preferably your own). Applying the four design principles we talked about today, redesign that resume. Send it to me before next week's class.

Read the following:

Clean Up Your Mess: A Guide to Visual Design for Everyone

Design Principles for News Apps and Graphics

A 20 Minute Intro to Typography Basics

Thinking with Type (there's a ton here, it's mostly meant as a resource to skim through. Focus on the sections about letter and text.)

Bring this:

One example of a design that you like (or hate)... it could be a website, a magazine, a poster, or anything else. Come prepared to talk about why you like it (or don't), and what design principles it uses (or doesn't use).

CLASS TWO: OCT 15th

Type, Color, and The Grid

An introduction to Illustrator: How to organize the bits and pieces of any design— typefaces, colors, words, pictures, columns, units, etc — to create a unifed whole.

← Lecture

Good typography and organized layouts can help you build better designs that inform, inspire, entertain and above all, communicate ideas clearly. We'll cover the basics of type classification (you know, the serif and sans-serif stuff), talk about some do's and don'ts of font choices and combinations, and review bits of Thinking with Type by Ellen Lupton.

Thinking with Type

Type Classification/Families p 42-47

Screen Fonts p 55

Kerning/Tracking/Line Spacing/Alignment p 80-85

Hierarchy p 94-95

We'll talk a little bit about color theory and how to pick color schemes (with a few online tools its not too hard to find gorgeous and informative color combinations). One of the best places to start is Color Brewer by Cynthia Brewer. We'll also delve into a very practical idea and technique for building great designs: the grid. We'll talk about units, columns and thirds, and how to go about translating those grids from paper to the web. We'll look at lots of examples from the Layout Workbook by Kristin Cullen.

Layout Workbook

Grid Systems p 54 - 71

Composition p 77-87

Designing with Type p 98-115

In Class

To try it all out, we're going to work through this tutorial:

Let's Make A Chart: Intro to Illustrator.

For reference, here is a more detailed explanation of Illustrator tools.

After Class

Do this:

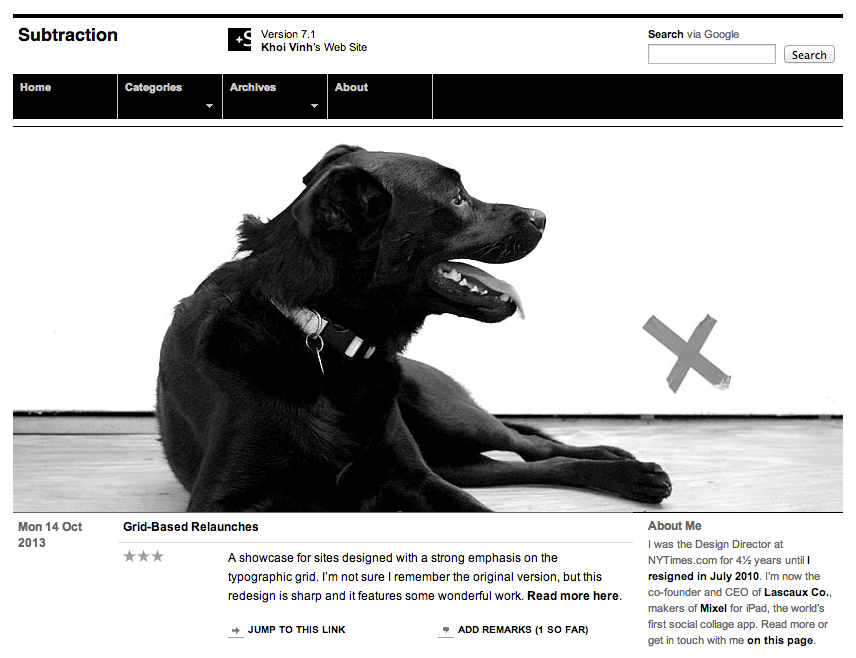
Re-create this image as best you possibly can using Illustrator.

(Hint: start by breaking it up into lines, squares, and text-boxes, and repeat). It's actually the homepage of designer Khoi Vinh, who relied heavily on a grid-based system for his website, and talks about grids often.

Watch this:

Get introduced to HTML and CSS! Watch part 2-6 of the Don't Fear the Internet video series. For those of you who are familiar with HTML/CSS, this should be review. For others, this is a great introduction!

Send me this:

1 to 2 ideas for your final project. Remember this can be a new project (I'd highly recommend building yourself an online portfolio if you don't already have one) or a project that you've been assigned in another class that could benefit from a design overhaul.

More resources/articles

Clearview: The Road to Clarity

The Art & Science of Communicating through Type

Five simple steps to better typography

Web Design is 95% Typography

Designing With Grid-Based Approach

Grid Anatomy

Kuler Color Wheel

Color Oracle

In Introduction to Adobe Illustrator

Illustrator Tools

CLASS THREE: OCT 29th

Design for the Web

How to structure and style any webpage with HTML and CSS. Plus a review of Illustrator for those who want more practice, and a few cool tricks with Photoshop.

← Lecture

Before CLASS

Make sure you have the following:

A text editor like TextWrangler (free), TextMate or Sublime Text

A Dropbox account

The latest version of Chrome

In CLASS

We're going to jump right into how to structure and style webpages with HTML and CSS. We'll review the basics so you're comfortable with everything from <p> tags to CSS classes. Then we'll create our very own web page from scratch.

HTML

Tags & Attributes

Classes & Id's

CSS

Selectors

Inheritance & Specificity

External Stylesheets

We'll meet the web inspector, which is basically like viewing the source code of a web page but much more awesome. We'll fiddle around with some existing web pages to alter some text, change styles and find image url's or raw data. Finally, we'll use Adobe Photoshop to do some image correction and created optimized images for the web.

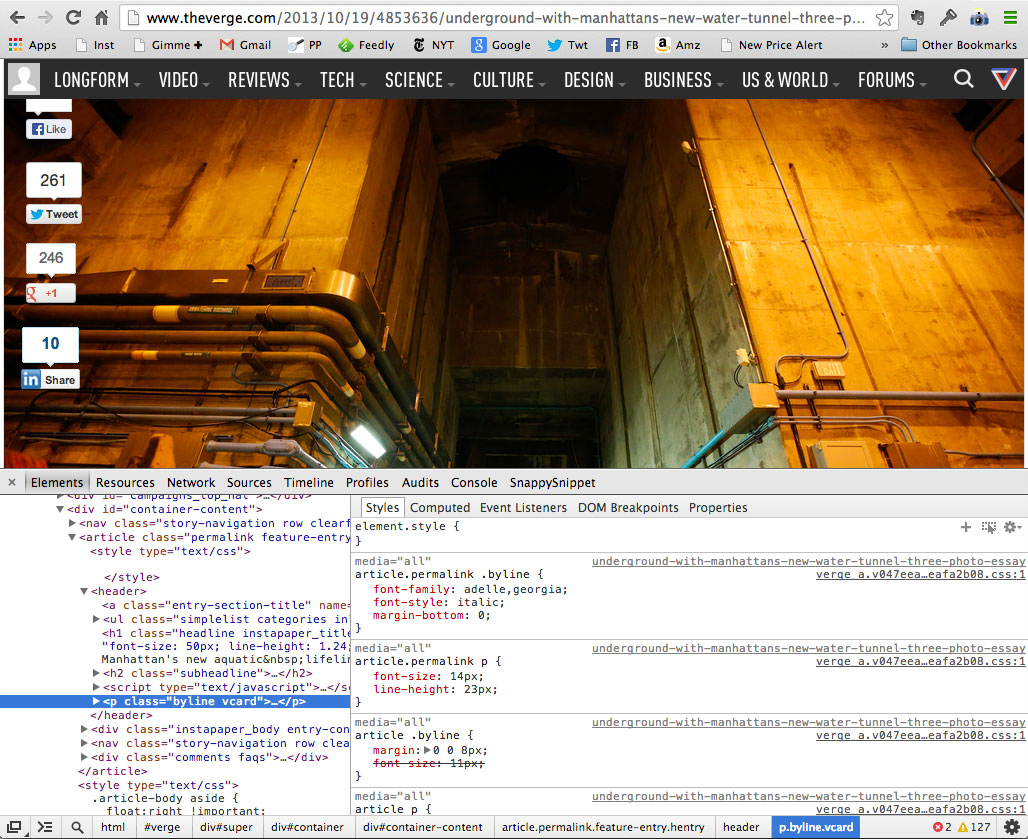
Web Inspector

Raw Source Code

The DOM

Manipulating Styles

Finding Files, Images and Data

Exercises

Let's Make a Webpage!

Meet Your Web Inspector (we'll be using this awesome tutorial from journo-developer Dan Nguyen)

Fun with Images in Photoshop

After Class

Read this:

An introduction to usability & interaction design: Affordances in Graphic Design, by Donald Norman

Send me this:

A rough sketch of your final project (you can use pen and paper or do a basic mockup Illustrator or HTML/CSS, depending on your comfort level with each of those tools).

Resources/articles

Intro to Web Fundamentals by Scott Murray

HTML Beginner tutorial

CSS Beginner tutorial

The 30 CSS Selectors you Must Memorize

Meet Your Web Inspector by Dan Nguyen

Getting Started with Photoshop

CLASS FOUR: OCT 30TH, Make Up Class

Interaction Design, Usability & Navigation

How to approach design from the user's perspective.

← Lecture

IN Class

We'll talk about how to create clear and intuitive designs for better user experiences. We'll focus on the basics: how to convey the basic idea of a page (what is this?), orient the user (where am I?), and make sure functions are self-evident (what do I do here?). We'll cover some common mistakes to avoid and a few easy steps to ensure usable interfaces and good navigation.

We'll start with some principles from a must-read book for anyone who deals with design and technology in the world (or has trouble opening doors): The Design of Everyday Things by Donald Norman. I promise that in addition to doors, you will never look at stovetops or teapots the same way.

The Design of Everyday Things

Having a Good Conceptual Model

Visibility

Mapping

Feedback

We'll talk about the value in signposts and breadcrumbs, how to use visual hierarchy to tell users the big idea, and why you should probably stick to conventions (something about a wheel and re-inventing). We'll look at some examples from something more web-specific: Don't Make Me Think by Steve Krug.

Don't Make me Think

Billboard Design 101

Omit Needless Words

Street Signs & Breadcrumbs

After Class

Keep working on your projects. If it's a print project in Illustrator, Photoshop or InDesign, think about how to get as far as you can with just the simple tools we talked about. You can go far with just the rectangle and type tool! If it's an online project or portfolio, think about how users will navigate between elements smoothly (will they scroll? click through?) Think about what you want users to see first and how you want to display your work (all at once? in a slideshow?). Try applying each of the 4 design principles in turn, consider font choices and color, and think about how to make interactions simple and intuitive.

Resources/Articles

Interdisciplinary Interaction Design by James Pannafino

The Psychological Basis for UI Design Rules

Interaction Design Tactics For Visual Designers

CLASS FIVE: NOV 5TH

Information Graphics, Data Visualization & Final Projects

How to design with data.

← Lecture

IN CLASS

We'll go on a quick tour of how to approach the visual display of information, from how to pick the right chart form to what it means to "tell a story" with data anyways (hint: lots of smart people disagree). The rest of the time we'll work on final projects.

AFTER CLASS

Send me your final projects. And that's it! Congrats on completing Design & Presentation. Best of luck in your future designs, and may improper kerning forever annoy you.